Difference between revisions of "Engine compression"
Old Hippie (talk | contribs) |
|||
| (5 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
[[Category:Terminology]] <!-- Leave this line --> | [[Category:Terminology]] <!-- Leave this line --> | ||
| − | + | {{Template:TopWiki}} <!-- Do not remove this line --> | |
| − | + | [[Image:4-Stroke-Engine-with-airflows.gif|right]] | |
| − | |||
| − | |||
| − | {{Template: | ||
| − | |||
| − | |||
| − | |||
| Line 16: | Line 9: | ||
== Effect and typical ratios == | == Effect and typical ratios == | ||
| + | |||
A high compression ratio is desirable because it allows an engine to extract more mechanical energy from a given mass of air–fuel mixture due to its higher [[thermal efficiency]]. This occurs because internal combustion engines are [[heat engine]]s, and higher compression ratios permit the same combustion temperature to be reached with less fuel, while giving a longer expansion cycle, creating more mechanical power output and lowering the exhaust temperature. | A high compression ratio is desirable because it allows an engine to extract more mechanical energy from a given mass of air–fuel mixture due to its higher [[thermal efficiency]]. This occurs because internal combustion engines are [[heat engine]]s, and higher compression ratios permit the same combustion temperature to be reached with less fuel, while giving a longer expansion cycle, creating more mechanical power output and lowering the exhaust temperature. | ||
| − | ===Gasoline | + | ===Gasoline engines=== |
| − | In production [[gasoline]] ( | + | |
| + | In production [[gasoline]] (petrol) engines from the past 20 years, compression ratios are typically between 8∶1 and 12∶1. Several production engines have used higher compression ratios, including: | ||
* Cars built from 1955–1972 which were designed for high-[[octane]] [[Tetraethyllead|leaded gasoline]], which allowed compression ratios up to 13∶1. | * Cars built from 1955–1972 which were designed for high-[[octane]] [[Tetraethyllead|leaded gasoline]], which allowed compression ratios up to 13∶1. | ||
| − | * Some Mazda [[SkyActiv]] engines released since 2012 have compression ratios up to 14.0∶1. | + | * Some Mazda [[SkyActiv]] engines released since 2012 have compression ratios up to 14.0∶1. The SkyActiv engine achieves this compression ratio with ordinary unleaded gasoline through improved scavenging of exhaust gases (which ensures cylinder temperature is as low as possible before the intake stroke), in addition to direct injection. |
| − | * The 2014 | + | * The 2014 Ferrari 458 Speciale also has a compression ratio of 14.0∶1. |
When [[forced induction]] (e.g. a [[turbocharger]] or [[supercharger]]) is used, the compression ratio is often lower than [[naturally aspirated engine]]s. This is due to the turbocharger/supercharger already having compressed the air before it enters the cylinders. Engines using [[port fuel-injection]] typically run lower boost pressures and/or compression ratios than [[direct injected]] engines because port fuel injection causes the air/fuel mixture to be heated together, leading to detonation. Conversely, directly injected engines can run higher boost because heated air will not detonate without a fuel being present. | When [[forced induction]] (e.g. a [[turbocharger]] or [[supercharger]]) is used, the compression ratio is often lower than [[naturally aspirated engine]]s. This is due to the turbocharger/supercharger already having compressed the air before it enters the cylinders. Engines using [[port fuel-injection]] typically run lower boost pressures and/or compression ratios than [[direct injected]] engines because port fuel injection causes the air/fuel mixture to be heated together, leading to detonation. Conversely, directly injected engines can run higher boost because heated air will not detonate without a fuel being present. | ||
| − | Higher compression ratios can make gasoline | + | Higher compression ratios can make gasoline engines subject to [[engine knocking]] (also known as "[[detonation]]", "pre-ignition" or "pinging") if lower octane-rated fuel is used. This can reduce efficiency or damage the engine if knock sensors are not present to modify the ignition timing. |
=== Diesel engines === | === Diesel engines === | ||
| − | [[Diesel engines]] use higher compression ratios than | + | [[Diesel engines]] use higher compression ratios than Gasoline engines, because the lack of a [[spark plug]] means that the compression ratio must increase the temperature of the air in the cylinder sufficiently to ignite the diesel. Compression ratios are often between 14∶1 and 23∶1 for direct injection diesel engines, and between 18∶1 and 23∶1 for [[indirect injection]] diesel engines. |
Since diesel engines operate on the principle of [[compression ignition]], a fuel which resists [[autoignition]] will cause late ignition, which can lead to engine knock. Diesel engines have a higher peak combustion temperature than gasoline engines, but the greater expansion means they eject less heat in their cooler exhaust. | Since diesel engines operate on the principle of [[compression ignition]], a fuel which resists [[autoignition]] will cause late ignition, which can lead to engine knock. Diesel engines have a higher peak combustion temperature than gasoline engines, but the greater expansion means they eject less heat in their cooler exhaust. | ||
=== Other fuels === | === Other fuels === | ||
| − | The compression ratio may be higher in engines running exclusively on [[LPG]] | + | The compression ratio may be higher in engines running exclusively on [[LPG]] or [[compressed natural gas]], due to the higher octane rating of these fuels. |
| − | === | + | === Racing engines === |
| − | [[ | + | [[Racing]] engines often run on high octane gasoline and can therefore use higher compression ratios. For example, motorcycle racing engines can use compression ratios as high as 14.7∶1, and it is common to find motorcycles with compression ratios above 12.0∶1 designed for 86 or 87 octane fuel. F1 engines come closer to 17∶1, which is critical for maximizing volumetric/fuel efficiency at around 18,000 RPM. |
Ethanol and methanol can take significantly higher compression ratios than gasoline. Racing engines burning [[methanol]] and [[ethanol fuel]] often have a compression ratio of 14∶1 to 16∶1. | Ethanol and methanol can take significantly higher compression ratios than gasoline. Racing engines burning [[methanol]] and [[ethanol fuel]] often have a compression ratio of 14∶1 to 16∶1. | ||
| − | + | <!-- NEED TO INSTALL MATH EXTENSION TO WORK | |
== Mathematical formula == | == Mathematical formula == | ||
In a [[piston engine]], the static compression ratio (<math>CR</math>) is the ratio between the volume of the [[Cylinder (cylinder]] and combustion chamber when the piston is at the [[bottom dead center|bottom of its stroke]], and the volume of the combustion chamber when the piston is at the [[top dead center|top of its stroke]]. | In a [[piston engine]], the static compression ratio (<math>CR</math>) is the ratio between the volume of the [[Cylinder (cylinder]] and combustion chamber when the piston is at the [[bottom dead center|bottom of its stroke]], and the volume of the combustion chamber when the piston is at the [[top dead center|top of its stroke]]. | ||
| Line 61: | Line 56: | ||
Because of the complex shape of <math>V_c</math> it is usually measured directly. This is often done by filling the cylinder with liquid and then measuring the volume of the used liquid. | Because of the complex shape of <math>V_c</math> it is usually measured directly. This is often done by filling the cylinder with liquid and then measuring the volume of the used liquid. | ||
| − | + | --!> | |
==Variable compression ratio engines== | ==Variable compression ratio engines== | ||
{{Variable compression ratio}} | {{Variable compression ratio}} | ||
| Line 68: | Line 63: | ||
Higher loads require lower ratios to increase power, while lower loads need higher ratios to increase efficiency, i.e. to lower fuel consumption. For automotive use this needs to be done as the engine is running in response to the load and driving demands. | Higher loads require lower ratios to increase power, while lower loads need higher ratios to increase efficiency, i.e. to lower fuel consumption. For automotive use this needs to be done as the engine is running in response to the load and driving demands. | ||
| − | The 2019 | + | The 2019 Infiniti QX50 is the first commercially available car that uses a variable compression ratio engine. |
== Relationship with the pressure ratio == | == Relationship with the pressure ratio == | ||
| Line 81: | Line 76: | ||
|| 2.64∶1 || 4.66∶1 ||9.52∶1 || 25.12∶1 || 44.31∶1 || 66.29∶1 || 90.60∶1 || 145∶1 | || 2.64∶1 || 4.66∶1 ||9.52∶1 || 25.12∶1 || 44.31∶1 || 66.29∶1 || 90.60∶1 || 145∶1 | ||
|} | |} | ||
| − | + | <!-- NEED TO INSTALL MATH EXTENSION TO WORO | |
This relationship is derived from the following equation: | This relationship is derived from the following equation: | ||
: <math>P_1 V_1^\gamma = P_2 V_2^\gamma \Rightarrow | : <math>P_1 V_1^\gamma = P_2 V_2^\gamma \Rightarrow | ||
\frac{P_2}{P_1}= \left( \frac{V_1}{V_2} \right)^\gamma </math> | \frac{P_2}{P_1}= \left( \frac{V_1}{V_2} \right)^\gamma </math> | ||
: where <math>\gamma</math> is the [[ratio of specific heats]] (air: approximately 1.4) | : where <math>\gamma</math> is the [[ratio of specific heats]] (air: approximately 1.4) | ||
| − | + | --!> | |
However, in most real-life internal combustion engines, the ratio of specific heats changes with temperature and that significant deviations from adiabatic behavior will occur. | However, in most real-life internal combustion engines, the ratio of specific heats changes with temperature and that significant deviations from adiabatic behavior will occur. | ||
| Line 94: | Line 89: | ||
The dynamic compression ratio is higher with more conservative intake [[camshaft timing]] (i.e. soon after BDC), and lower with more radical intake camshaft timing (i.e. later after BDC). Regardless, the dynamic compression ratio is always lower than the static compression ratio. | The dynamic compression ratio is higher with more conservative intake [[camshaft timing]] (i.e. soon after BDC), and lower with more radical intake camshaft timing (i.e. later after BDC). Regardless, the dynamic compression ratio is always lower than the static compression ratio. | ||
| + | <!-- | ||
The absolute cylinder pressure is used to calculate the dynamic compression ratio, using the following formula: | The absolute cylinder pressure is used to calculate the dynamic compression ratio, using the following formula: | ||
: <math>P_\text{cylinder} = P_\text{atmospheric} \times \text{CR}^\gamma</math> | : <math>P_\text{cylinder} = P_\text{atmospheric} \times \text{CR}^\gamma</math> | ||
| − | : where <math>\gamma</math> is a [[Polytropic process|polytropic]] value for the [[ratio of specific heats]] for the combustion gasses at the temperatures present (this compensates for the temperature rise caused by compression, as well as heat lost to the cylinder) | + | : where <math>\gamma</math> is a [[Polytropic process|polytropic]] value for the [[ratio of specific heats]] for the combustion gasses at the temperatures present (this compensates for the temperature rise caused by compression, as well as heat lost to the cylinder) --!> |
Under ideal (adiabatic) conditions, the ratio of specific heats would be 1.4, but a lower value, generally between 1.2 and 1.3 is used, since the amount of heat lost will vary among engines based on design, size and materials used. For example, if the static compression ratio is 10∶1, and the dynamic compression ratio is 7.5∶1, a useful value for cylinder pressure would be 7.5<sup>1.3</sup> × atmospheric pressure, or 13.7 [[bar (unit)|bar]] (relative to atmospheric pressure). | Under ideal (adiabatic) conditions, the ratio of specific heats would be 1.4, but a lower value, generally between 1.2 and 1.3 is used, since the amount of heat lost will vary among engines based on design, size and materials used. For example, if the static compression ratio is 10∶1, and the dynamic compression ratio is 7.5∶1, a useful value for cylinder pressure would be 7.5<sup>1.3</sup> × atmospheric pressure, or 13.7 [[bar (unit)|bar]] (relative to atmospheric pressure). | ||
| Line 103: | Line 99: | ||
| − | {{Template: | + | {{Template:BottomWikiHippieAds}} <!-- Do not remove this line --> |
== [[References]] == | == [[References]] == | ||
| + | *https://en.wikipedia.org/wiki/Compression_ratio | ||
* | * | ||
Latest revision as of 00:58, 10 May 2023
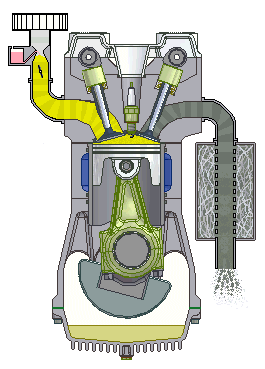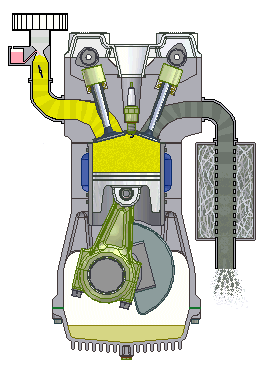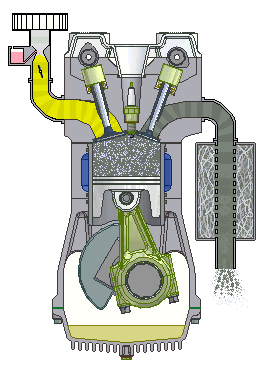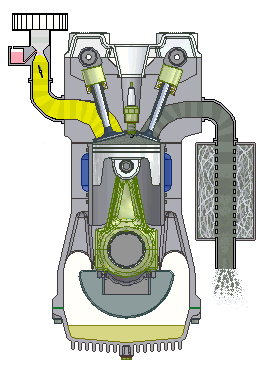
In a combustion engine, the static compression ratio is calculated based on the relative volumes of the combustion chamber and the cylinder. It is a fundamental specification for combustion engines. The dynamic compression ratio is a more advanced calculation which also takes into account gasses entering and exiting the cylinder during the compression phase.
Most engines used a fixed compression ratio, however a variable compression ratio engine is able to adjust the compression ratio while the engine is in operation. The first production engine with a variable compression ratio was introduced in 2019.
Contents
Effect and typical ratios
A high compression ratio is desirable because it allows an engine to extract more mechanical energy from a given mass of air–fuel mixture due to its higher thermal efficiency. This occurs because internal combustion engines are heat engines, and higher compression ratios permit the same combustion temperature to be reached with less fuel, while giving a longer expansion cycle, creating more mechanical power output and lowering the exhaust temperature.
Gasoline engines
In production gasoline (petrol) engines from the past 20 years, compression ratios are typically between 8∶1 and 12∶1. Several production engines have used higher compression ratios, including:
- Cars built from 1955–1972 which were designed for high-octane leaded gasoline, which allowed compression ratios up to 13∶1.
- Some Mazda SkyActiv engines released since 2012 have compression ratios up to 14.0∶1. The SkyActiv engine achieves this compression ratio with ordinary unleaded gasoline through improved scavenging of exhaust gases (which ensures cylinder temperature is as low as possible before the intake stroke), in addition to direct injection.
- The 2014 Ferrari 458 Speciale also has a compression ratio of 14.0∶1.
When forced induction (e.g. a turbocharger or supercharger) is used, the compression ratio is often lower than naturally aspirated engines. This is due to the turbocharger/supercharger already having compressed the air before it enters the cylinders. Engines using port fuel-injection typically run lower boost pressures and/or compression ratios than direct injected engines because port fuel injection causes the air/fuel mixture to be heated together, leading to detonation. Conversely, directly injected engines can run higher boost because heated air will not detonate without a fuel being present.
Higher compression ratios can make gasoline engines subject to engine knocking (also known as "detonation", "pre-ignition" or "pinging") if lower octane-rated fuel is used. This can reduce efficiency or damage the engine if knock sensors are not present to modify the ignition timing.
Diesel engines
Diesel engines use higher compression ratios than Gasoline engines, because the lack of a spark plug means that the compression ratio must increase the temperature of the air in the cylinder sufficiently to ignite the diesel. Compression ratios are often between 14∶1 and 23∶1 for direct injection diesel engines, and between 18∶1 and 23∶1 for indirect injection diesel engines.
Since diesel engines operate on the principle of compression ignition, a fuel which resists autoignition will cause late ignition, which can lead to engine knock. Diesel engines have a higher peak combustion temperature than gasoline engines, but the greater expansion means they eject less heat in their cooler exhaust.
Other fuels
The compression ratio may be higher in engines running exclusively on LPG or compressed natural gas, due to the higher octane rating of these fuels.
Racing engines
Racing engines often run on high octane gasoline and can therefore use higher compression ratios. For example, motorcycle racing engines can use compression ratios as high as 14.7∶1, and it is common to find motorcycles with compression ratios above 12.0∶1 designed for 86 or 87 octane fuel. F1 engines come closer to 17∶1, which is critical for maximizing volumetric/fuel efficiency at around 18,000 RPM.
Ethanol and methanol can take significantly higher compression ratios than gasoline. Racing engines burning methanol and ethanol fuel often have a compression ratio of 14∶1 to 16∶1.